Projections and Survey Systems

Contents

A. Projections

B. Coordinate Systems

C. Survey Systems

A. Projections

1. Background

You can't squash a grapefruit peel flat without breaking it into many pieces (try it sometime). In the same way, we cannot transfer the spherical surface of Earth to a flat surface without distortion. We can create a logical way to transfer coordinates from the sphere onto a flat map. Such ways of transferring coordinates are known as projections, after the original method of transferring by literally projecting a light through a globe onto a surface. But no projection can accomplish its task without some distortion. Fortunately, we can choose to preserve certain qualities that a globe possesses. But in the process we sacrifice other qualities.

Before we project the actual Earth onto a surface, we usually simplify it. Earth isn't a perfect sphere. It's somewhat flattened at the Poles, so an ellipsoid represents Earth better (an ellipsoid is formed by rotating an ellipse around one of its axes). Actually, the diameter at the equator is only about 42.8 km more than the polar axis. But it is enough to throw off exacting measurements, like property lines.

An ellipsoid is still not perfect; the geoid is an irregular, but even closer, representation of Earth. It's the equivalent of mean sea level all over the globe. Since gravity and Earth's surface are irregular, the geoid is not a smooth surface, and can't be represented with equations easily, so it's rarely used for mapping.

A particular ellipsoid, with particular values for equatorial and polar diameters, is often used in projecting and measuring on Earth, particularly for highly accurate measuring such as in surveying. A dozen ellipsoids are in common use around the world, including:

• Clarke Spheroid of 1866, used in most of the North America. It was revised earlier this century, with the results called the North American Datum of 1927, or NAD27.
• Geodetic Reference System 1980, a new ellipsoid, is being adopted in North America to correct inaccuracies in NAD27. The resulting "datum" is called the North American Datum of 1983, or NAD83.
• International Ellipsoid, from 1924, used in most of the rest of the world (but developed in the US from US data!).

2. Methods of Projection

Many projections can be visualized as literally projecting a light source through a transparent globe onto a surface. The light source can be any number of places - at the center of the globe, at the opposite side of Earth, or out in space, for instance (see figure below for examples). The map surface onto which the projection is made can be various shapes, and can also be at various places. In all projections, the map surface touches the globe at at least one point. This is because any map is most accurate where it touches the globe; there is no distortion here. The contact point between globe and map is called the point of tangency; if it is a line, it's a line of tangency, standard line, or (if it is a parallel) standard parallel. Away from the tangent locations, the map surface gets further from the globe, and hence more distorted. Most all projections nowadays are done by computer using equations that relate lat/long to x/y coordinates on the map.

Projections may be made onto three basic shapes, with three types of projections resulting:

a. Planar

Also called azimuthal. In this case, the globe is projected onto a flat surface. The "light source" can be from several locations. Usually, the flat surface touches the globe at a single point. Most often planar projections are used for Polar regions, and the tangent point is the North or South Pole.

b. Cylindrical

Here a cylinder is wrapped around the globe, usually with the map surface touching the globe at a circle (a great circle, to be exact -- a circle whose center coincides with the center of Earth). Cylindrical projections are the only one of the three main types that can show the entire globe, and so most world maps are cylindrical.

The most famous cylindrical projection is the one named for Gerhardus Mercator, who developed it in 1569. It was valuable for early navigators, since straight lines on a Mercator map are also compass headings. Unfortunately, it greatly distorts the sizes of areas near the Poles (see section 3 below), so it should not be used as a general--purpose world map!

c. Conical

The third type of projection is made onto a cone. Usually this means contacting the globe along one of the parallels (lines of latitude), i.e., a small circle. Although we cannot use conic projections for a world map, they are excellent for continent--sized areas in the mid--latitudes. Most maps of the United States are made with conic projections.

Conic projections are usually made more accurate by "sinking" the cone part way into the globe (remember, this is all done with computers, not literally!). Then we have two lines of tangency, or two standard parallels, along which the map is extremely accurate. This two--line approach is also called the secant case, as opposed to the simple tangent case. You may see maps of the US with a statement on the bottom like: "Lambert Conformal Conic Projection, 48° and 33° Standard Parallels." The projection was developed by J.H. Lambert (1728--1777), an important figure in cartography.

d. Other

Some projections are not based on any of the above three shapes, and cannot be visualized as literally being projected. Instead, they simply have equations that tell where to plot each latitude/longitude coordinate from the globe. Some examples are the Sinusoidal and van der Grinten projections. World maps are often made with these projections, since they may have less distortion than cylindrical projections.

3. Qualities of Projections

The other major factor you need to know about a projection is the qualities about the globe that the projection either preserves or distorts. Most projections can preserve one or more of the following qualities, but none can retain all of them. Note that the projection method (planar, cylindrical, or conical) does not necessarily mean any of these qualities below are preserved or distorted. It all depends on how the projection is done.

a. Equal-Area

Some projections show all areas in true proportion to their real areas on the globe. For example, a dime placed on the map would cover the same area regardless of where placed. To show areas truly, a map must distort most of the other qualities below, at least subtlely. But if you need a general--purpose map of the world or continental area, an equal--area map, or a map that is very close to equal--area, is your best bet. Some examples: Sinusoidal, Albers Conic Equal--Area, and Lambert Azimuthal Equal--Area.

b. True Shape, or Conformality

Another important characteristic of the globe that can be distorted on a map is the shape of areas. This distortion problem is obvious on a cylindrical map that is equal--area, because the higher latitudes near the Poles have to be distorted to preserve areas. The Mercator projection is conformal, but at the expense of area. The Mercator shows Greenland almost as large as South America, when in reality it is about 1/8 the continent's size. Some people have accused developed nations (which are mostly in the higher northern latitudes) of intentionally portraying their lands as larger than developing countries (which are mostly in lower, tropical latitudes). One projection, known as the Peters projection, has been promoted as the "true" world map, since it shows countries with true areas. Peters is indeed equal--area, but does a number on shape-as one person put it, it makes the world look like it was hung on a laundry line. Many other equal--area projections are available that do a better job with shape.

c. True Scale

In no map can you use one scale accurately for the whole map. Some distortion occurs, although it is slight in many maps. Some projections can preserve true scale and distance along one or more lines. These are may be called equidistant projections. A popular planar projection for polar areas is known as the Azimuthal Equidistant, which has true scale from the central tangent point-the Pole-to any other point on the map. You could also use an Azimuthal Equidistant map centered on your location to measure distances accurately to any other place on the globe. Some map software can draw such a map for you.

d. True Direction

The last major quality of maps is direction. Maps that preserve it are called azimuthal. Most planar projections preserve true direction away from the center of the map (usually the Pole) and so azimuthal is nearly synonymous with planar projection.

e. Other Qualities

Some projections are designed to have specialized qualities. The Mercator projection is one: all constant compass headings (rhumb lines, or loxodromes) are straight lines. The Gnomonic projection is another: all great circle routes are straight lines. As you may know, great circle routes are the shortest distances between points on the globe. For example, when you fly from San Francisco to London, you don't fly along a parallel of latitude, but over the polar route; this is along a great circle. If you're flying or sailing, then, you can combine the gnomonic and Mercator maps for navigating. First you draw your route on the gnomonic map (a straight line connecting the two places), then transfer the route to the Mercator map as a series of straight segments that approximate the gnomonic line. This way, you can follow the straight segments on the Mercator map with a compass, and turn only when you need to follow the next segment. You may notice this when you're flying and the pilot periodically turns to follow these segments.

B. Coordinate Systems

How can we describe locations on Earth? If someone asks you, "where is Hawaii?", what do you tell them? You can give them directions relative to your position ("swim 2000 miles south--southwest"). Other ways are also possible, but what if you needed to pinpoint a location for people coming from many directions? Or if you wanted to record a location for later reference? Or if you had no landmarks to guide you? This is the purpose of coordinate systems. They are ways of describing locations on Earth in reference to an established grid. You have probably been exposed to the most common method, latitude/longitude, but there are many other methods in use.

1. Latitude & Longitude

The latitude and longitude system is also called the geographical grid. This grid exploits the fact that Earth is nearly a sphere, and that it spins on an axis. Looking down on the globe from above the North Pole, we can fit a circle to the rotating Earth. We could assign each location along any circle that surrounds the Pole a measurement in degrees. A circle has 360 degrees. We could use this range of numbers, going from 0° to 360°. Alas, early map--makers didn't do this, exactly. They wanted low numbers on both sides of the Prime Meridian (the 0 line). As a result, the globe is divided into hemispheres, each assigned longitude between 0° and 180°, with the addition of East or West to differentiate the halves. The lines of longitude are meridians.

To complement the east--west measurement, a north--south measurement is necessary, so that we may pinpoint locations. Since we only need to measure along one meridian, we only need to assign measures to a half--circle, or 180 degrees. Once again, it's more complicated than necessary. Rather than go from 0° at the North Pole to 180° at the South Pole (or vice--versa), the system starts with 0° at the halfway point (the Equator), and measures north and south to 90° at the Poles. Each line of latitude is a circle; these lines are called parallels (sensible, since they are parallel to one another).

With this system we can pinpoint any location on Earth. Since a degree of latitude spans about 111 km, each degree can be broken down to get more exact. A degree is composed of 60 minutes (60'), and a minute is composed of 60 seconds (60') -- just like a clock. Based on this system, SSU lies at 38° 20' 46" N, 122° 40' 30" W. If you're uncomfortable with this system, you should practice looking up locations on a globe or atlas.

Lat/long is cumbersome to use for at least two reasons. First, notice that meridians converge at the Poles. A degree of longitude decreases from about 111 km at the Equator to 0 at the Poles; 1° is about 88 km in Sonoma County. Convergence makes lat/long poor for use as a rectangular grid, where we want simple x,y coordinates for locations. Second, lat/long is not a decimal system. How far is it from 114° 34' 54" to 116° 14' 33"? Not very far, but you'd have trouble giving me the distance even in terms of degrees/minutes/seconds. For these reasons, lat/long is usually replaced by other coordinate systems, especially at the local level, for most descriptions of location. Most of these systems, including those below, use a projection of the globe onto a flat surface, onto which we can then draw an x/y grid.

2. State Plane Coordinates (SPC)

The National Geodetic Survey developed the SPC system beginning in 1933. Eventually every state was covered, with coordinates identified both on maps and on the ground, so that surveyors and cartographers could accurately identify and measure locations. The key to this system is that rather than having one coordinate system for the entire US, separate systems were assigned to smaller zones. Each zone used its very own projection and coordinate center and system. 120 zones cover the US. Within each zone, you are never far from the standard line. This way, the coordinates would be extremely accurate within each zone (less than 1 foot per 10,000 feet of measurement, in fact). The problem, of course, is that coordinates between zones don't match up, so the SPC system is not useful for small--scale (large--area) maps that include more than one zone.

Nearly all states have multiple zones, but zones never cross county lines. California has 7 zones, most extending as east--west bands; Sonoma County's zone extends to Lake Tahoe. Los Angeles County has its own zone (naturally). Each state uses either the Lambert Conformal Conic or the Transverse Mercator projection (California uses the first).

Within each zone, locations are identified by x,y coordinates in feet. Any x,y coordinate system needs an origin, that is, where the coordinates are (0,0). In order to keep all SPC numbers positive, the origin for each zone is placed off to the southwest of the actual zone covered. This origin is not the actual center of the projection (that is, where the globe "touches" the sheet projected onto). That actual center is in the middle of each SPC zone, so that coordinates are most accurate there. In short, the actual center is assigned an arbitrarily large coordinate (such as 2,000,000 feet East, 400,000 feet North), and all other coordinates are measured from there. This puts the "false origin" off to the southwest.

SPC coordinates are shown on all USGS topographic maps. Usually tick marks on the margins of the map show regular spacing of the grid, and selected marks have the actual coordinates in feet. By examining the topographic map for Cotati, we can find that the SPCs for SSU are 1,806,500' E, 246,200' N. As mentioned above, the SPC system is used widely in conducting local land surveying and public works. It can be used by the cartographer and geographer not only to identify coordinates of places, but to calculate distances between locations by use of the Pythagorean Theorem, as described in the next section.

3. Universal Transverse Mercator (UTM)

The UTM grid is similar to the SPC system, at least regarding how you use it at the local level and in being marked on all USGS topographic maps. The principal differences are that the coordinates are given in meters, not feet, and that the zones are much larger. UTM zones extend north--south, practically from Pole to Pole. The UTM grid system covers the entire globe (well, almost - except for very near the Poles).

You encountered the Mercator projection before. In the standard Mercator, the cylinder is "wrapped" around the Equator, and areas become very distorted toward the Poles. A transverse Mercator projection turns the cylinder, so that the circle of contact with the globe is around a pair of meridians. This way, the projection is very accurate on a north--south zone near the standard line. Of course, once again it distorts severely at large distances away from the meridian.

The Universal Transverse Mercator grid gets around the distortion problem by the same method as the SPC system. The UTM has many zones, each with its own projection centered on a meridian. There are 60 zones to be exact, each 6° wide (which covers Earth, 60 x 6° = 360° around). Within each zone, then, the grid is very accurate in matching true Earth distance and direction. As with the SPC system, going across zones is difficult, so the UTM is meant primarily for local and regional measurement.The UTM was adopted and thus popularized by the Army in 1947. The Army included the UTM grid on its topographic maps; later the USGS added UTM coordinates to most of its maps and photoquads. The Army numbered each 6°--wide zone around the globe from 1 to 60, starting at 180° W and going east; northern California is in zone 10. They also lettered north--south segments of each zone from A (south) to Z (north). The north--south segments aren't necessary, and so are rarely used outside the military.

Within each UTM zone, x,y coordinates can be given in meters. Like SPCs, an origin is needed, and is placed outside the zone off the southwest corner. The north--south center of the zone is arbitrarily designated as 500,000 meters east (that is, east of a false origin off to the west). "Eastings" (x--coordinates) for locations east of the center are higher than this, up to about 850,000 m E; westward the coordinates decrease, down to about 150,000 m E; the zone doesn't extend all the way to the false origin. The "northing," or north--south (y) coordinate, depends on which hemisphere you're in. For the Northern Hemisphere part of each zone, the measurement starts at the Equator with 0 and measures the number of meters north (up to about 8,800,000 m N at 80° N). In the Southern Hemisphere, the Equator is designated arbitrarily as 10,000,000 m N, and coordinates decrease as you go south toward the South Pole.

Examples: A location with coordinates 334,400 m E, 4,203,600 m N would be 334,400 meters east of the false origin, or (500,000 -- 334,400 =) 165,600 meters west of the central line. It would be 4,203,600 meters, or 4,203.6 km, north of the Equator. The UTM coordinates for SSU are: 4,243,540 m E, 528,390 m N (these are actually close to the coordinates for Stevenson 3065).

The UTM grid is shown on all recent USGS topographic maps. The latest topographic maps draw in the grid as thin black lines. All topos with the UTM have tick marks along the margin, along with values for eastings or northings next to most ticks. Except for a few values near the corners, the easting or northing value is abbreviated . For example, instead of printing "3,445,000 m N", the tick would be labeled 3445, with the thousands and meters--north assumed from the context.

The UTM grid, even if drawn in on the map, may not give us the exact coordinates for a given location. Even on 7 1/2--minute quads, the grid is only every 1,000 meters (1 km). How can you determine coordinates more precisely? The answer is called a roamer. This is simply a sheet of paper, plastic or other material that has finer distance intervals marked off that match the scale of the map. Starting from the nearest grid lines, you can measure over to the location and come close (at least within 100 m) to the actual easting and northing coordinates.

Another big advantage of the UTM (or SPC) grid is that once you have coordinates for two locations within the same zone, calculating the distance between them is simple. Just apply the Pythagorean Theorem. If the two locations are at the coordinates (x1, y1) and (x2, y2), then the distance (D) between them is:

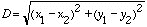
For example, say you find coordinates for two cities: Springfield at 294,100 m E, 3,428,900 m N, and Garden City at 292,400 m E, 3,428,100 m N. The distance between them is then:

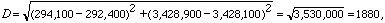
that is, the distance is 1880 meters, or 1.88 kilometers.

As you can see, the UTM grid is a very useful system for tracking Earth locations. It is used extensively in remote sensing, computerized mapping, and geographic information systems. It is worth your while to familiarize yourself with it.

C. Survey Systems

A related topic to coordinate systems is how we describe the boundaries of parcels of land. SPC or UTM coordinates are great for giving locations of points, but less so for describing area. You can describe a parcel by going from point to point--this is the first method below. But other methods are easier in some circumstances. This section covers land-description methods used in the US. An important fact about survey systems is that once land is surveyed under a given system, that's it--the description of the land stays with it permanently. Land within old Spanish Land Grants in California still retain their descriptions based on the original survey.

1. Metes-and-Bounds

Early settlers in the Thirteen Colonies used the same method for dividing and describing land as they had in the Old World (especially England). This system is known as metes__-and-bounds. The idea is very simple: a land parcel is described based on going from one point to another, in a polygon that encompasses the parcel. For example, a legal description might read:

"Commencing from a point one-half mile upstream from Smith Bridge on Jones Creek, proceed northeast 500 feet to Spring Hill, then northwest to the large oak tree, then southwest to the large rock in the middle of Jones Creek, then along Jones Creek to the origin."

The first settlers in an area naturally claimed the best land, and set up boundaries that encompassed that land. Most of the time, this worked alright, and in a sense it shapes human use of the land according to the landscape itself, rather than imposing an artificial pattern on the land.

But metes-and-bounds surveys are liable to create problems. Since surveys were done as land was claimed, overlapping claims often resulted--with lengthy court battles ensuing. Even today, land titles are more difficult to verify in areas surveyed by metes-&-bounds. A bigger problem is that the boundary markers (oak tree, big rock) eventually are obliterated, with the boundaries becoming ambiguous. One measure to help has been to replace landmarks with exact compass directions and distances (also known as "Coordinate Geometry"). The description above might be replaced with:

"Commencing from a point one-half mile upstream from Smith Bridge on Jones Creek, proceed N 45° E 500 feet, then N 50° W 324 feet, then S 35° W to Jones Creek, then along Jones Creek to the origin."

A final problem with metes-&-bounds was that the US government wanted to sell off land in the West quickly, in order to raise cash (no income taxes back then). A system was needed that could quickly and rationally divide up the land, allowing for sales without a lot of legal wrangling. The US Public Land Survey, described below, became the US answer to the problem.

2. Spanish Land Grants

The Spanish, and later Mexicans, ruled California and much of the Southwest for about 300 years. They too parceled out land for use by colonists (with little regard to Native occupation, of course). The methods of description were very similar to metes-and-bounds. Much of the land was given or sold to large landowners for ranchos as Spanish Land Grants. These land grants usually focused on water resources, which are scarce in the West; sometimes the system is called Spanish Riparian (riparian means relating to watercourses).

Much of the better land in California ended up in one of these land grants. Remember, once allocated, land continues to be described under its original survey, permanently. Even after California became part of the US, and land grant claims were honored (though sometimes exchanging hands under questionable deals). The land grants have be subdivided since then, but evidence still can be found in property descriptions, and on USGS topographic maps. For instance, some land grants in Sonoma County were Rancho Cabeza de Santa Rosa, Petaluma Rancho, and Rancho Cotate. These labels, along with their boundaries, can be found on topos for Sonoma County.

3. Other Irregular Surveys

Other survey methods were used in certain parts of the US. In Louisiana and other areas settled by the French, long-lots were used. The land along important lanes of commerce, usually rivers, was divided into narrow strips extending back into the interior. This resulted in a series of long but narrow plots of land that are still evident on topo sheets of Louisiana, coastal Texas, and Mississippi River towns, even as far upstream as Wisconsin.

4. The US Public Land Survey (PLS)

The majority of the land in the US is described under the US Public Land Survey (PLS) System. After independence, the US wanted to dispose quickly of lands in the West (at that time, land between the 13 Colonies and the Mississippi River). Some form of logical, orderly system was inevitable, but the exact form took time to shape. Thomas Jefferson and others eventually worked out a rational, rectangular (squarish) survey, called the Public Land Survey (PLS) system, which was enacted under the Northwest Land Ordinance of 1785 (with later revisions).

The PLS starts out by establishing an x,y coordinate system for a given area. The north-south line is called a principal meridian, and the east-west line a baseline. Each baseline is given a unique name, so that each land parcel can be identified by that name. The area described based on a principal meridian/baseline pair varies from a small part of a state (e.g., eastern Ohio, northwestern California), to several states (e.g., the Fifth Principal Meridian covers most of Arkansas, Missouri, Iowa, Minnesota, and most of the Dakotas).

California has three principal meridian/baseline pairs: the San Bernardino Meridian (southern California), Mt. Diablo Meridian (most of northern California), and the Humboldt Meridian (northwestern corner of the state).

The initial point is the intersection of the principal meridian and baseline. From this point, townships are marked off east/west and north/south. Each township is 6 miles on a side, or 36 square miles. Townships are designated on the east-west direction as being a certain number of Ranges east or west of the principal meridian. The township is also a certain number of Townships north or south of the baseline (note the dual use of the term township, as an area and as a coordinate). For example, the township that is just on the northeast corner of the initial point is Township 1 North, Range 1 East, usually abbreviated T. 1 N, R. 1 E. Or T. 3 S, R. 2 W would be the third township south of the baseline and two townships to the west.

Each township had to be divided, since few people could afford 36 mi². The division was into 36 sections, one square mile each. Rather than using an x,y system here, the sections were simply numbered consecutively from 1 to 36, starting in the northeast corner and snaking around the rows, with 36 at the southeast corner.

Most land purchases were for less than one section; the Homestead Act of 1863 allowed people to receive one-quarter section if lived on by the claimant. Sections can be broken down into halves or quarters, each part designated by a compass direction. If divided in half, we have either east/west halves, or north/south halves. If divided into quarters, we have the NE, NW, SW, and SE quarters. Quarters can be broken down further if necessary, for example we might have the NE quarter of the SE quarter.

A square mile contains 640 acres, so a quarter section has 160 acres, a quarter-quarter 40 acres, and so on. The typical Midwestern farm used to be a quarter section, or 160 acres. Farms have been consolidated over the past several decades, so the typical farm occupies closer to a square mile, especially in California.

A complete property description must include all of these breakdowns into township, section, and fraction of section (if less than an entire section). A typical property description in a PLS area might read:

USGS topographic maps indicate PLS townships and ranges along the margins. Section and township lines are shown on the map itself with red lines, and sections are numbered in red. You will no doubt notice on some topos that the PLS townships and sections end abruptly in some part of the map. This is common around Santa Rosa. This is because these non-PLS lands were in Land Grants before 1846, when California became part of the US. Remember, once surveyed, never again.

The PLS has had a dramatic impact on the American landscape. Since all land is divided into squares, the landscape itself looks very square. You'll notice this when flying over the middle part of the US, where topography does not interfere with its effects as much. It also contributed to the isolation of farm families in the 19th Century, who lived on their own square farms far from neighbors. Contrast this to French surveyed-lands, where people live much closer together. Our survey system no doubt contributed to the ideal of American individualism.

A final note about the PLS--it's far from a perfect system. There are many irregularities, which are especially noticeable in certain regions. Section and township lines are not always exactly north/south and east/west, and sections are sometimes less than a full square mile (they're then called government lots, or fractional lots). The irregularities derive from several sources:

• Meridians converge to the north, so as surveyors moved north, townships didn't match up with those further south. Often east-west correction lines were set up, along which townships were re-aligned. You'll notice this effect when driving north or south along a country road and you have to take a sudden turn right or left, then turn north/south again after a short distance.
• Surveying in wet or mountainous terrain is difficult, and lines often went astray. Once set up, however, the errors were kept, and lines remained askew.
• Surveyors were paid by the number of sections surveyed, so hurried surveyors weren't always careful surveyors.
• Some surveyors simply weren't careful, or were even staggering-drunk on the job.

Because of these irregularities, the PLS is not a great system for computerized map coordinates when you want a regular x,y grid. Use the UTM or SPC grid instead.

5. Other Rectangular Surveys

Some states weren't touched at all by the PLS: the original 13 Colonies (and subsequent split-offs: West Virginia, Vermont, Maine), Tennessee, Kentucky, and Texas. Some New England towns used a modified rectangular survey when settled. Some of the states had considerable land left to dispose of in the 19th Century, and developed their own rectangular survey for these lands. Texas, in particular, used several variations on a rectangular survey, some of which used Spanish units. These rectangularly-surveyed areas look like PLS areas as you travel over them, even though officially they're not.